فهرست مطالب
ضریب تغییر پاسخ به دلیل شکلپذیری شبکه صفحه سیستم دیوار ICF در مناطق با خطر لرزهای بالا
Pouria Asadi*, Rahmat Madandoust**, Seyed Mehdi Zahrai***
دریافت در ۱۷ اکتبر ۲۰۱۴ / تجدید نظر در ۱۴ دسامبر ۲۰۱۴ / پذیرش در ۱۰ فوریه ۲۰۱۵ / انتشار آنلاین ۱۴ مارس ۲۰۱۶
چکیده مقاله رفتارهای لرزه ای آی سی اف ICF
قالب بتن عایق (ICF) شامل قالب های دائمی است که معمولاً فوم پلی استایرن منبسط شده است. قالب های عایق بتنی یک قالب برای بتن ایجاد می کند که به عنوان عایق دائمی ساختمان در جای خود باقی می ماند. سازه ها معمولاً تغییر شکل های پلاستیکی را در طول زلزله های بزرگ تجربه می کنند. با این حال، به دلیل پیچیدگی انجام تجزیه و تحلیل غیرخطی، کدها اثرات رفتار غیر کشسان را از طریق ضرایب کاهش (R) در نظر می گیرند و به جای آن امکان تحلیل خطی را می دهند. ضریب کاهش برای سیستم دیواری Screen- Grid ICF (SGICF) تاکنون ارائه نشده است. در این تحقیق عوامل کاهش شکلپذیری سیستمهای دیوار SGICF توسط تحلیل استاتیکی غیرخطی (Pushover) و مدل سازنده پلاستیک آسیبدیده بتن (CDP) در ABAQUS 6.12 تعیین میشوند. سپس نتایج با نتایج مدل تجربی مقایسه می شود. نتایج حاصل از این تحقیق نشان می دهد که چنین سیستم سازه ای در صورت استفاده در مناطق با خطر لرزه ای بالا، شکل پذیری قابل قبولی دارد.
۱_معرفی سیستم سازه ای آی سی اف ICF
سیستمهای ICF اساساً شامل قالبهای دائمی هستند که معمولاً فوم پلی استایرن منبسط شده است. سپس بتن به داخل حفره پمپ می شود تا عنصر ساختاری دیوارها را تشکیل دهد. در این سیستم از قسمتهایی از قالبهای عایق برای دیوارهای باربر و دیوارهای غیرباربر برای پی و بالاتر استفاده میشود.در ادامه تصویری از حین بتن ریزی دیوار ICF را مشاهده می کنید.

این قطعات برای دیوارهای داخلی و خارجی، لنگه و دیوارهای بتنی ساده یا مسلح برای پی و دیوار حائل زیرزمین استفاده می شود. پس از بتن ریزی، این قطعات در جای خود باقی می مانند.
سه دسته از سیستم های ICF بر اساس شکل حاصل از دیوار بتنی تشکیل شده وجود دارد. برخلاف دیوار ICF تخت، در سیستم دیواری Screen-Grid ICF (SGICF)، فضای زیادی بین لایه ها با اتصال دهنده های عظیم اشغال می شود. این کانکتورها با قطعات یکپارچه هستند، بنابراین بررسی اثرات این حفره ها ضروری است.
تحقیقات متعددی در مورد رفتار دیوارهای ICF انجام شده است. مطالعات زیر بیشتر تحقیقات مربوطه در مورد سیستم SGICF را نشان می دهد. آنها نیاز به مطالعات بیشتر به ویژه برای به دست آوردن پارامترهای طراحی لرزه ای را نشان داده اند.
کی و دوسیکا در آزمایشگاه تحقیقات و تست زیرساخت دانشگاه ایالتی پورتلند در پورتلند، اورگان، دیوارهای SGICF را بررسی کردند (کی و دوسیکا، ۲۰۰۹). دیوارها تحت بارگذاری سیکلی استاتیکی درون صفحه قرار گرفتند. شکست دیوارهای آزمایش با ترک خوردگی برشی مورب از طریق هسته های عمودی در امتداد یک صفحه افقی منفرد سازگار بود.
مطالعه سیستم های ICF در SGICF توسط مرکز تحقیقاتی انجمن ملی سازندگان خانه (NAHB) برای وزارت مسکن و شهرسازی ایالات متحده انجام شد (مرکز تحقیقاتی NAHB، Inc.، ۲۰۰۱). هدف محققان تعیین ضخامت دیواره پیوسته معادل برای ارتباط با سیستم SGICF بود.
دیوارهای SGICF نیز توسط محرابی برای انجمن سیمان پرتلند مورد مطالعه قرار گرفت (مهرابی، ۲۰۰۰). محرابی قاب فولادی، قاب چوبی، دیوار ICF مسطح، دیوار ICF شبکه وافل و دیوارهای SGICF را مقایسه کرد. پانل ها از نظر مقاومت برشی با هدف مقایسه کفایت آنها در مناطق زلزله ۱ یا ۱ مورد آزمایش قرار گرفتند.
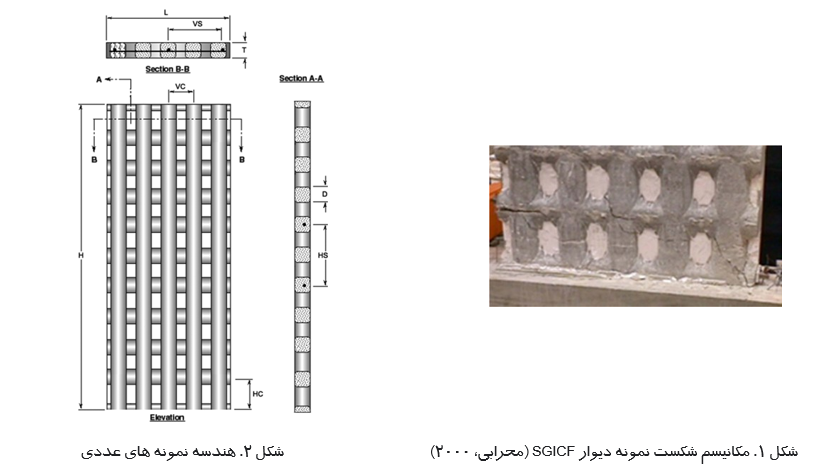
آنها دریافتند که دیوار SGICF نسبتاً ۶.۵ تا ۸ برابر قوی تر و سفت تر از دیوارهای پانل اسکلت چوبی و فولادی با ابعاد یکسان است. شکل ۱ حالت خرابی دیوار ICF شبکه نمایشگر آزمایش شده را نشان می دهد (محرابی، ۲۰۰۰).
مطالعه ای توسط مرکز تحقیقات ساختمان و مسکن (BHRC) یک دیوار SGICF در مقیاس کامل را بررسی کرد (محمد کاری و خلیلی جهرمی، ۲۰۱۰). دیوارها تحت بارگذاری چرخه ای درون صفحه قرار گرفتند. هدف محققین تعیین تأثیر فضاهای خالی بر عملکرد دیوارهای SGICF بود. تصدیق رفتار سیستم سازه ای در فاز پلاستیک که نشان دهنده قابلیت های سیستم سازه ای در جذب انرژی است، برای استفاده در مناطق با سطوح بالای خطر لرزه ای مهم است.
عدم انجام مطالعات تجربی و عددی بر روی سیستم های SGICF و نگرانی در مورد قابلیت های سیستم دیواری SGICF به ویژه شکل پذیری سیستم، گسترش گسترده را محدود کرده است.
استفاده از این سیستم تا کنون، شکل پذیری و عوامل اصلاح پاسخ برای سیستم های دیواری SGICF ارائه نشده است. در این تحقیق یک مطالعه عددی برای تعیین شکلپذیری و ضریب اصلاح پاسخ سیستمهای دیواری SGICF انجام شده و سپس نتایج با نمونههای آزمایشی مقایسه میشود. نتایج این تحقیق شکلپذیری و ضریب اصلاح پاسخ ناشی از شکلپذیری سیستم دیوار SGICF را نشان میدهد.
۲_تحلیل عددی رفتار لرزه ای آی سی اف ICF
نمونههای عددی مورد بررسی در این تحقیق بر اساس روش پیشبینی برای عایقسازی قالبهای بتنی در ساختوسازهای مسکونی ویرایش دوم (NAHB Research Center, Inc., 2002) با توجه به مفاد ردههای طراحی لرزهای C و D (مناطق لرزهای ۳ و ۴) طراحی شدهاند.
فرض بر این است که نمونه های عددی در سطح زمین یک ساختمان دو طبقه قرار دارند. طول نمونه های عددی ۱.۲۹ متر، ارتفاع ۳ متر و ضخامت ۰.۱۵ متر است. شکل ۲ جزئیات ساختاری پانل دیواری SGICF را نشان می دهد. این نقشه ابعاد و جزئیات تقویت کننده پانل SGICF را نشان می دهد، اما اشکال بتن عایق را نشان نمی دهد. پانل دیوار بتنی شامل یک شبکه یکپارچه از پنج بند عمودی (ستون) و نه کامل، به علاوه دو نوار افقی (تیر) بود. سیستم های SGICF باید حداقل ضخامت اسمی بتن ۱۵۲ میلی متر برای اعضای بتنی افقی و عمودی (هسته ها) داشته باشند. هسته های عمودی و افقی باید حداکثر ۳۰۵ میلی متر فاصله داشته باشند. (NAHB Research Center, Inc., 2002).
برای طراحی لرزه ای رده های D1 و D2، حداقل مقاومت فشاری بتن، fc، باید ۲۰.۶۸ مگاپاسکال مطابق با ASTM C 31 و ASTM C 39 باشد. در رده های طراحی لرزه ای D1 و D2، فولاد تقویت کننده باید الزامات ASTM A706 را برآورده کند. فولاد کم آلیاژ
حداقل مقاومت تسلیم فولاد تقویت کننده باید درجه ۴۰ (۳۰۰ مگاپاسکال) باشد. حداقل آرماتور عمودی و افقی باید یک میلگرد #۱۶ (قطر اسمی: ۱۶ میلیمتر) در ۶۱۰ میلیمتر و یک میلگرد #۱۶ با حداکثر فاصله ۴۵۷ میلیمتر در مرکز باشد. خواص و انواع آرماتورهای فولادی استفاده شده در جدول ۱ نشان داده شده است.
۳_خواص مواد و مدل سازی در آی سی اف ICF
مدل ساختاری پلاستیسیته آسیب دیده بتن (CDP) برای مدلسازی بتن در نرم افزار ABAQUS استفاده می شود (Hibbitt et al., 2012). این مدل با توجه به نتایج تحقیقات انجام شده توسط Lubliner (Lubliner, 1989) و Lee and Fenves (Lee and Fenves, 1998) در نرم افزار ABAQUS توسعه یافته است. مدل CDP قابلیت شبیهسازی رفتار غیرکشسان در فشار/کشش را دارد و میتواند خواص آسیب را در بتن نشان دهد.
در مدل CDP فرض شده است که دو مکانیسم اصلی آسیب بتن ترک خوردگی و خرد شدن بتن در کشش و فشار است (Hibbitt et al., 2012).

مفهوم پلاستیسیته آسیب همسانگرد برای شبیه سازی رفتار غیرکشسانی بتن استفاده می شود. معادله (۱) و (۲) به ترتیب روابط بین تنش و کرنش بتن تحت بار کششی و فشاری را ارائه می دهند.

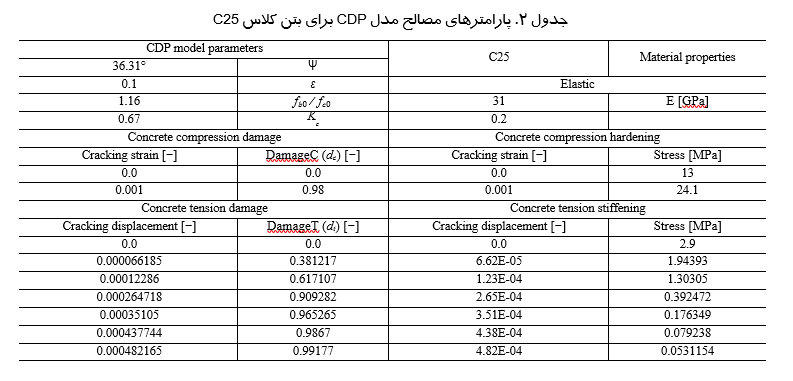
در معادلات بالا، E0 مدول یانگ بتن در کشش و فشار، dt و dc، شاخصهای آسیب بتن در کشش و فشار و کرنشهای پلاستیکی معادل در کشش و فشار هستند. در این تحقیق از بتن C25 برای مدل سازی نمونه های عددی استفاده شده است. پارامترهای مورد نیاز برای مدلسازی بتن با استفاده از مدل CDP در جدول ۲ ارائه شده است (Hibbitt et al., 2012).
در شبیهسازی حاضر، آرماتور در بتن بهعنوان عناصر خرپایی گسسته تعبیهشده متصل به ناحیه بتن مدلسازی شده است (مالم، ۲۰۰۹). میلگردهای فولادی با توجه به موقعیت ها و فواصل مشخص شده در جدول ۱ و شکل ۲ به صورت عمودی و افقی در دیوار بتنی قرار گرفتند.
در این تحقیق از گریدهای فولادی ۴۰ و ۶۰ برای مدلسازی میلگردهای فولادی استفاده شده است. رفتار الاستیک مواد فولادی با مشخص کردن مدول یانگ (E) و نسبت پواسون (ν) تعریف میشود که مقادیر معمول آن به ترتیب ۲۱۰ GPa و ۰.۳ است. رفتار پلاستیک به شکل جدولی، شامل تنش تسلیم واقعی، و کرنش پلاستیک مربوطه تعریف میشود. تنش واقعی و کرنش لگاریتمی باید تعریف شوند (Hibbitt et al., 2012). مقادیر ورودی تنش در هر نقطه برای یک ماده همسانگرد با توجه به معادلات محاسبه می شود. (۳) و (۴). شکل ۳ منحنی های تنش-کرنش پلاستیک واقعی را نشان می دهد.
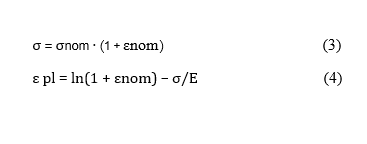
به منظور مدلسازی دیوار بتنی ICF در نرم افزار آباکوس ۸
آجر سه بعدی خطی گره، یکپارچگی کاهش یافته و المان کنترل ساعت شنی C3D8R و برای مدل سازی آرماتور از المان خرپا سه بعدی خطی ۲ گره T3D2 استفاده شد. مدل کلاسیک پلاستیسیته فلز برای تعریف رفتار غیرخطی آرماتور مورد استفاده قرار گرفت (Hibbitt et al., 2012).
Ψ= زاویه اتساع است که در صفحه p-q اندازه گیری می شود.
ε= گریز از مرکز پتانسیل جریان است
fb0 ⁄ fc0= نسبت تنش تسلیم فشاری هم محوری اولیه و تنش تسلیم فشاری تک محوری اولیه است.
kc = نسبت تنش ثابت دوم در نصف النهار کششی به نصف النهار فشاری برای هر مقدار تعریف شده از متغیر فشار در تسلیم اولیه است.
dc = پارامتر آسیب فشاری است.
dt = پارامتر آسیب تنش است.
بارگذاری با اعمال شرایط مرزی جابجایی در بالاترین سطح نمونه های عددی U1 به جابجایی هدف و U2 = 0 انجام شد. شرایط مرزی در پایین ترین سطح نمونه های عددی با تثبیت درجات آزادی U1، U2، U3، UR1، UR2 اعمال شد. UR3 = 0. برای بررسی اثر مش بندی بر نتایج به دست آمده، نمونه های عددی با مش های درشت و ریز مورد مطالعه قرار گرفتند. تعداد المانها و تعداد گرههای با مشهای ظریف به ترتیب ۱۷۲۶۷ و ۲۳۵۸۵ بود. تعداد المانها و تعداد گرههای دارای مش به ترتیب ۴۳۱۴ و ۶۹۲۱ بود.
۴_ تأیید نتایج لرزه ای آی سی اف ICF
برای تایید نتایج عددی، مدلی با خواص هندسی و مکانیکی مطابق با نمونه آزمایش شده در مرکز تحقیقات NAHB
( NAHB Research Center, Inc., 2001) در نظر گرفته شد.

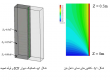
برای این منظور، نمونه عددی با طول ۱.۲ متر، ارتفاع ۲.۴ متر و ضخامت ۰.۱۵۲ متر با نام ICFPATH مدلسازی شد. خواص مواد، تکنیک مدلسازی، شرایط مرزی و بارگذاری این نمونه عددی مانند سایر نمونههای عددی است که در قسمت قبل به تفصیل توضیح داده شد. منحنی برشی-جابجایی پایه نمونه عددی ICFPATH و نمونه تجربی در شکل ۴ نشان داده شده است.

نتایج عددی نشان می دهد که حداکثر بار مقاومت شده توسط مدل عددی ۷۱.۷۸ کیلو نیوتن و جابجایی متناظر ۰.۰۳۹ متر است در حالی که برای مدل تجربی، حداکثر بار ۷۶.۵۱ کیلونیوتن و جابجایی متناظر ۰.۰۴۳ متر است. علاوه بر این، در مدل عددی، بار شکست ۵۸.۳۱۷ کیلونیوتن و جابجایی مربوطه ۰.۰۴۶ متر است در حالی که برای مدل تجربی، بار شکست ۶۲.۷۲ کیلونیوتن و جابجایی متناظر ۰.۰۵۱ متر است. هر دو نمونه تجربی و عددی با یک حالت شکست برشی معمولی رفتار مشابهی داشتند.
شکل ۵ عریض شدن و انتشار ترک ها از گوشه بارگیری را نشان می دهد که باعث شکست در نمونه های تجربی و عددی شده است. مقایسه نتایج عددی و تجربی نشاندهنده سازگاری و دقت قابل قبول نتایج عددی است.
۵_ عوامل اصلاح پاسخ
ضریب اصلاح پاسخ معمولاً بر حسب دو جزء اصلی آن بیان میشود: ضریب کاهش شکلپذیری (Rµ) و ضریب مقاومت بیش از حد سازه (Ω) (Uang, 1991). فاکتور R به صورت زیر تعریف می شود:
R = Rµ× Ω (۵)
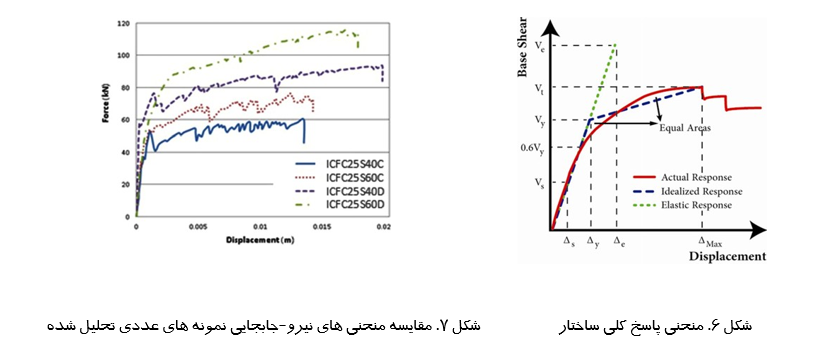
اجزای ضریب اصلاح پاسخ با استفاده از شکل ۶ به شکل زیر تعریف شده است:
Rµ =Ve/Vy (۶)
Ω=Vy/Vs (۷)
فاکتور R سپس می تواند به عنوان بازسازی شود:
R= Rµ ×Ω= Ve/Vy × Vy/Vs=Ve/Vs (۸)
جایی که، Ve، Vy و Vs به ترتیب با مقاومت پاسخ الاستیک سازه، مقاومت تسلیم ایدهآل، و مقاومت تسلیم قابل توجه اول مطابقت دارند. در این تحقیق از روش پیشنهادی FEMA (FEMA-356, 2000) برای ارزیابی ضریب اصلاح پاسخ برای سیستم دیوار SGICF استفاده شده است. در این مطالعه، جابجایی هدف مربوط به نقطه ای است که افت مقاومت معادل ۱۵ درصد حداکثر مقاومت است (کاپوس و پنلیس، ۱۹۹۷).
۱-۵ :ضریب تغییر پاسخ به دلیل شکل پذیری، R μ در سیستم آی سی اف ICF
ضریب اصلاح پاسخ به دلیل شکلپذیری سیستم دیواره ICF شبکه صفحه نمایش در مناطق با خطر لرزهای بالا
نیومارک و هال (نیومارک و هال، ۱۹۹۵) مجموعه ای از معادلات ۱۰ تا ۱۲ را توسعه دادند که Rµ را بر حسب نسبت شکل پذیری سازه، µ، که بر حسب حداکثر رانش سازه، ∆max، و رانش متناظر با حالت ایده آل بیان می شود، تعریف می کند. نقطه تسلیم، ∆y، به صورت:
µ=∆max/∆y (۹)
Rµ= µ دوره طولانی (۱۰)
R=√۲µ-۱ دوره میانی (۱۱)
Rµ=۱ دوره کوتاه (۱۲)
۶_ تجزیه و تحلیل نتایج
برای تجزیه و تحلیل مدل از حل کننده استاندارد نرم افزار آباکوس (ABAQUS/Standard) استفاده شد. برای به دست آوردن منحنی تغییر مکان برشی پایه سازه، جابجایی به بالاترین سطح سازه از طریق روش گام به گام اعمال شد. این تغییر مکان با تعریف شرایط مرزی به عنوان تغییر مکان در جهت در نظر گرفته شده بر سازه تحمیل شد. نمونه های عددی بررسی شده توسط ABAQUS/Standard برای رسیدن به جابجایی هدف مربوط به نقطه ای که در آن افت مقاومت معادل ۱۵ درصد حداکثر مقاومت است بارگذاری شدند (Kappos and Penelis, 1997).
۱-۶: واکنش نیرو-جابجایی در سیستم آی سی اف
پاسخ نمونه های عددی به تاریخچه جابجایی در منحنی های نیرو-جابجایی شکل ۷ نشان داده شده است. منحنی های جابجایی نیرو نشان می دهد که پاسخ نمونه عددی اساساً در طول بارگذاری اولیه خطی بوده و با افزایش جابجایی غیرخطی شده است. رابطه جابجایی نیرو بین برش پایه و جابجایی گره کنترل باید با یک رابطه ایده آل برای محاسبه سختی جانبی موثر و مقاومت تسلیم موثر دیوار جایگزین شود.
پاره خط های روی منحنی جابجایی نیروی ایده آل باید با استفاده از یک گرافیک تکرار شونده قرار گیرند
روشی که تقریباً ناحیه بالا و پایین منحنی را متعادل می کند.
سختی جانبی موثر باید به عنوان سختی سکانس محاسبه شده در نیروی برشی پایه برابر با ۶۰ درصد مقاومت تسلیم موثر سازه در نظر گرفته شود. یک قطعه خط که از منحنی واقعی در جابجایی هدف محاسبه شده عبور می کند باید شیب پس از تسلیم را تعیین کند. استحکام تسلیم موثر نباید بیشتر از حداکثر نیروی برشی پایه در هر نقطه در امتداد منحنی واقعی در نظر گرفته شود (FEMA-356، ۲۰۰۰).
نرم افزاری با استفاده از زبان برنامه نویسی پاسکال برای پردازش نتایج به دست آمده از تجزیه و تحلیل نمونه های عددی توسعه یافته است. کد توسعهیافته، جابجایی منحنی غیرخطی برشی پایه را به منحنی دوخطی سادهشده طبق رویه ارائهشده در FEMA 356 تبدیل میکند. علاوه بر این، کد، نقطه مربوط به پاسخ الاستیک را به دقت محاسبه میکند، بر اساس فرض نیومارک و هال، که در نظر میگیرد که وجود دارد. تعادل انرژی بین پاسخ الاستیک و پاسخ غیر خطی سازه های کوتاه. نرمافزار توسعهیافته، دادههای منحنیهای برشی جابجایی پایه بالایی را برای نمونههای عددی بررسیشده نشاندادهشده در شکل ۷ پردازش میکند. اطلاعات حاصل در جدول ۳ وارد شد. نسبت شکلپذیری (µ) نمونههای عددی با استفاده از معادله تعیین شد. (۹). سپس ضریب اصلاح پاسخ ناشی از شکلپذیری (µ) محاسبه شد. با استفاده از معادله ارائه شده توسط نیومارک و هال، ضریب اصلاح پاسخ محاسبه شده برای نمونه های عددی مورد بررسی به دلیل شکل پذیری در جدول ۳ نشان داده شده است.
دیوارهای مورد بررسی دارای شکل پذیری ۵.۴ تا ۷.۸ هستند. بنابراین این سیستم سازه ای شکل پذیری قابل قبولی برای استفاده در مناطق زلزله خیز دارد. همانطور که در شکل ۸ (الف) نشان داده شده است، نسبت شکل پذیری (µ) نمونه های عددی مدل سازی شده برای قرار دادن در مناطقی که احتمال وقوع زلزله های بسیار شدید وجود دارد (D)، تا ۴۰ درصد بیشتر از نمونه های عددی مدل شده است. جهت استقرار در مناطقی که احتمال وقوع زلزله شدید (C) وجود دارد.
مقایسه حداکثر ظرفیت بار نمونه های عددی بررسی شده در شکل ۸ (ب) نشان داده شده است. مشاهده می شود که دیوار ICFC25S60D حداکثر بار ۱۱۸ کیلونیوتن را متحمل می شود.


این بار مربوط به جابجایی ۰.۰۱۸ متر است و پس از آن، ظرفیت بارگذاری دیوار به میزان قابل توجهی کاهش می یابد. حداکثر ظرفیت بار نمونه های عددی ICFC25S40D، ICFC25S60C و ICFC25S40C به ترتیب ۱۹.۸۴، ۳۴.۱۵ و ۴۸.۲۶ درصد کمتر از نمونه عددی ICFC25S60D است. درصد نسبت رانش نمونههای عددی مورد بررسی در لحظه گسیختگی برای نمونههای عددی طراحیشده برای رده لرزهای ۰.۴۶% و ۰.۴۷% و برای رده لرزهای D 0.67% و ۰.۶۱% است. مقادیر محاسبهشده ضریب اصلاح پاسخ (Rµ) برای نمونه های عددی به دلیل شکل پذیری در شکل ۸ (c) نشان داده شده است. ضریب اصلاح پاسخ به دلیل شکلپذیری (Rµ) نمونههای عددی مدلسازیشده و تحلیلشده برای کاربرد در مناطقی که احتمال وقوع زلزلههای بسیار شدید (D) وجود دارد، تا ۲۵ درصد بیشتر از نمونههای عددی برای قرار دادن در مناطقی است که وجود دارد. احتمال وقوع زلزله های شدید (C) است. که بیانگر اهمیت توجه دقیق به این معیار در روش پیش بینی برای استفاده از این سیستم سازه ای در مناطق با خطر لرزه ای بالا می باشد.
شکل ۹ ضرایب کاهش شکل پذیری (Rµ) را برای نمونه های عددی با استفاده از معادله معرفی شده توسط نیومارک و هال و معادله تئوری نشان می دهد. مقادیر به دست آمده از معادله نظری تقریباً ۵ درصد بیشتر از مقادیر بدست آمده از معادله نیومارک و هال است. این مقایسه دقت معادله نیومارک و هال را برای سازه های کم ارتفاع در دوره های کوتاه نشان می دهد.
۷_نتیجه گیری
نتایج حاصل از این تحقیق نشان می دهد که ضرایب کاهشی ناشی از شکل پذیری برای سیستم دیواری SGICF را می توان ۳.۱۵ در نظر گرفت. این سیستم سازه ای شکل پذیری ۵.۴ تا ۷.۸ دارد و در نتیجه شکل پذیری قابل قبولی برای استفاده در مناطق با خطر لرزه ای بالا دارد. نسبت شکلپذیری (µ) نمونههای عددی برای قرارگیری در مناطقی که احتمال وقوع زلزلههای بسیار شدید وجود دارد (D) تا ۴۰ درصد بیشتر از نمونههای عددی مدلسازیشده برای قرار دادن در مناطقی است که احتمال وقوع زلزلههای شدید وجود دارد (C). ضریب اصلاح پاسخ به دلیل شکلپذیری (Rµ) نمونههای عددی برای کاربرد در مناطقی که احتمال وقوع زلزلههای بسیار شدید وجود دارد (D) تا ۲۵ درصد بیشتر از نمونههای عددی برای قرار دادن در مناطقی است که احتمال وقوع زلزله های شدید وجود دارد (C). که بیانگر اهمیت رعایت دقیق این معیار در روش پیش بینی برای استفاده از این سیستم سازه ای در مناطق با خطر لرزه ای بالا می باشد.
منابع:
Davies, J. (1996). “Observation of fracture path development in mortar beam specimens.” Advn. Cem. Bas. Mat., Vol. 3, No. 1996, pp. 3136, DOI: 10.1016/S1065-7355(96)90067-X.
FEMA-356 (2000). Pre standard and commentary for the seismic rehabilitation of buildings, American Society of Civil Engineers: USA, Virginia
Hibbitt, D., Karlsson, B., and Sorensen, P. (2012). Inc., ABAQUS Theory Manual, ABAQUS Version 6.12
Kappos, A. J. and Penelis G. G. (1997). Earthquake-resistant concrete structures london, Taylor and Francis Group
Kay, T. and Dusicka, P. (2009). Reversed cyclic deformation tests on insulated concrete form walls using the APEX blocks interlocking system [report], Portland, ORLee, J. and Fenves, G. L. (1998). “Plastic-damage model for cyclic loading of concrete structures.” Journal of Engineering Mechanics, Vol. 124, No. 8, pp. 892-900, DOI: 10.1061/(ASCE)0733-9399 (1998)124:8(892)
Lubliner, J., Oliver, J., Oller, S., and Onate, E. (1989). “A plastic-damage model for concrete.” International Journal of Solids and Structures, Vol. 25, No. 3, pp. 229-326, DOI: 10.1016/0020-7683(89)90050-4.
Malm, R. (2009). Predicting shear type cracks initiation and growth in concrete with nonlinear finite elements methods, PhD Thesis, Royal Institute of Technology, Division of Structural Design and Bridges, Stockholm, Sweden.
Mehrabi, A. (2000). In-plane lateral load resistance of wall panels in residential buildings [report], Skokie, IL: Portland Cement
Association, PCA R&D Serial No. 2403.
Mohammad Kari, B. and Khalili Jahromi, K. (2010). Insulating concrete forms: Building and Housing Research Center Publication, Tehran, Research Report Publication No. 493.
NAHB (2001). Research center, inc., in-plane shear resistance of insulating concrete form walls [report], Upper Marlboro, MD
NAHB (2002). Research Center, Inc., Prescriptive method for insulating concrete forms in residential construction second edition (revised), Upper Marlboro, MD.
Newmark, N. M. and Hall, W. J. (1995). Structural response modification factors, Applied Technology Council, No. 19. Schlangen, E. (1993). Experimental and numerical analysis of fracture processes in concrete, PhD Thesis, Delft University of Technology.
Uang, C.-M. and Establishing, R. (1991). “(or Rw) and Cd factors for building seismic provisions.” Journal of Structural Engineering, Vol. 117, No. 1, pp. 19-28, DOI: 0733-9445(1991)117:1(19).
گرد آورنده: مهندس محمدرضا رمضانی